BaselearnerPSpline creates a spline base learner object. The object calculates the B-spline basis functions and in the case of P-splines also the penalty. Instead of defining the penalty term directly, one should consider to restrict the flexibility by setting the degrees of freedom.
Format
S4 object.
Arguments
- data_source
(InMemoryData)
Data object which contains the raw data (see?InMemoryData).- blearner_type
(
character(1))
Type of the base learner (if not specified,blearner_type = "spline"is used). The unique id of the base learner is defined by appendingblearner_typeto the feature name:paste0(data_source$getIdentifier(), "_", blearner_type).- degree
(
integer(1))
Degree of the piecewise polynomial (defaultdegree = 3for cubic splines).- n_knots
(
integer(1))
Number of inner knots (defaultn_knots = 20). The inner knots are expanded bydegree - 1additional knots at each side to prevent unstable behavior on the edges.- penalty
(
numeric(1))
Penalty term for P-splines (defaultpenalty = 2). Set to zero for B-splines.- differences
(
integer(1))
The number of differences to are penalized. A higher value leads to smoother curves.- df
(
numeric(1))
Degrees of freedom of the base learner(s).- bin_root
(
integer(1))
The binning root to reduce the data to \(n^{1/\text{binroot}}\) data points (defaultbin_root = 1, which means no binning is applied). A value ofbin_root = 2is suggested for the best approximation error (cf. Wood et al. (2017) Generalized additive models for gigadata: modeling the UK black smoke network daily data).
Usage
BaselearnerPSpline$new(data_source, list(degree, n_knots, penalty, differences, df, bin_root))
BaselearnerPSpline$new(data_source, blearner_type, list(degree, n_knots, penalty, differences, df, bin_root))Methods
$summarizeFactory():() -> ()$transfromData(newdata):list(InMemoryData) -> matrix()$getMeta():() -> list()
Inherited methods from Baselearner
$getData():() -> matrix()$getDF():() -> integer()$getPenalty():() -> numeric()$getPenaltyMat():() -> matrix()$getFeatureName():() -> character()$getModelName():() -> character()$getBaselearnerId():() -> character()
Details
The data matrix is instantiated as transposed sparse matrix due to performance
reasons. The member function $getData() accounts for that while $transformData()
returns the raw data matrix as p x n matrix.
Examples
# Sample data:
x = runif(100, 0, 10)
y = sin(x) + rnorm(100, 0, 0.2)
dat = data.frame(x, y)
# S4 wrapper
# Create new data object, a matrix is required as input:
data_mat = cbind(x)
data_source = InMemoryData$new(data_mat, "my_data_name")
# Create new linear base learner factory:
bl_sp_df2 = BaselearnerPSpline$new(data_source,
list(n_knots = 10, df = 2, bin_root = 2))
bl_sp_df5 = BaselearnerPSpline$new(data_source,
list(n_knots = 15, df = 5))
# Get the transformed data:
dim(bl_sp_df2$getData())
#> [1] 14 10
dim(bl_sp_df5$getData())
#> [1] 19 100
# Summarize factory:
bl_sp_df2$summarizeFactory()
#> Spline factory of degree 3
#> - Name of the used data: my_data_name
#> - Factory creates the following base learner: spline_degree_3
# Get full meta data such as penalty term or matrix as well as knots:
str(bl_sp_df2$getMeta())
#> List of 8
#> $ df : num 2
#> $ penalty : num 729953
#> $ penalty_mat: num [1:14, 1:14] 1 -2 1 0 0 0 0 0 0 0 ...
#> $ degree : num 3
#> $ n_knots : num 10
#> $ differences: num 2
#> $ bin_root : num 0
#> $ knots : num [1:18, 1] -2.587 -1.6952 -0.8033 0.0886 0.9804 ...
bl_sp_df2$getPenalty()
#> [,1]
#> [1,] 729953.1
bl_sp_df5$getPenalty() # The penalty here is smaller due to more flexibility
#> [,1]
#> [1,] 52.0648
# Transform "new data":
newdata = list(InMemoryData$new(cbind(rnorm(5)), "my_data_name"))
bl_sp_df2$transformData(newdata)
#> $design
#> 5 x 14 sparse Matrix of class "dgCMatrix"
#>
#> [1,] 0.1666667 0.66666667 0.1666667 . . . . . . . . . . .
#> [2,] 0.1666667 0.66666667 0.1666667 . . . . . . . . . . .
#> [3,] . 0.05295636 0.5818030 0.3599001 0.005340631 . . . . . . . . .
#> [4,] 0.1666667 0.66666667 0.1666667 . . . . . . . . . . .
#> [5,] 0.1666667 0.66666667 0.1666667 . . . . . . . . . . .
#>
bl_sp_df5$transformData(newdata)
#> $design
#> 5 x 19 sparse Matrix of class "dgCMatrix"
#>
#> [1,] 0.1666667 6.666667e-01 0.1666667 . . . . . . . . . . . . .
#> [2,] 0.1666667 6.666667e-01 0.1666667 . . . . . . . . . . . . .
#> [3,] . 9.687235e-05 0.2115857 0.6599926 0.1283248 . . . . . . . . . . .
#> [4,] 0.1666667 6.666667e-01 0.1666667 . . . . . . . . . . . . .
#> [5,] 0.1666667 6.666667e-01 0.1666667 . . . . . . . . . . . . .
#>
#> [1,] . . .
#> [2,] . . .
#> [3,] . . .
#> [4,] . . .
#> [5,] . . .
#>
# R6 wrapper
cboost_df2 = Compboost$new(dat, "y")
cboost_df2$addBaselearner("x", "sp", BaselearnerPSpline,
n_knots = 10, df = 2, bin_root = 2)
cboost_df2$train(200, 0)
#> Train 200 iterations in 0 Seconds.
#> Final risk based on the train set: 0.21
#>
cboost_df5 = Compboost$new(dat, "y")
cboost_df5$addBaselearner("x", "sp", BaselearnerPSpline,
n_knots = 15, df = 5)
cboost_df5$train(200, 0)
#> Train 200 iterations in 0 Seconds.
#> Final risk based on the train set: 0.02
#>
# Access base learner directly from the API (n = sqrt(100) = 10 with binning):
str(cboost_df2$baselearner_list$x_sp$factory$getData())
#> num [1:14, 1:10] 0.167 0.667 0.167 0 0 ...
str(cboost_df5$baselearner_list$x_sp$factory$getData())
#> num [1:19, 1:100] 0 0 0 0 0 ...
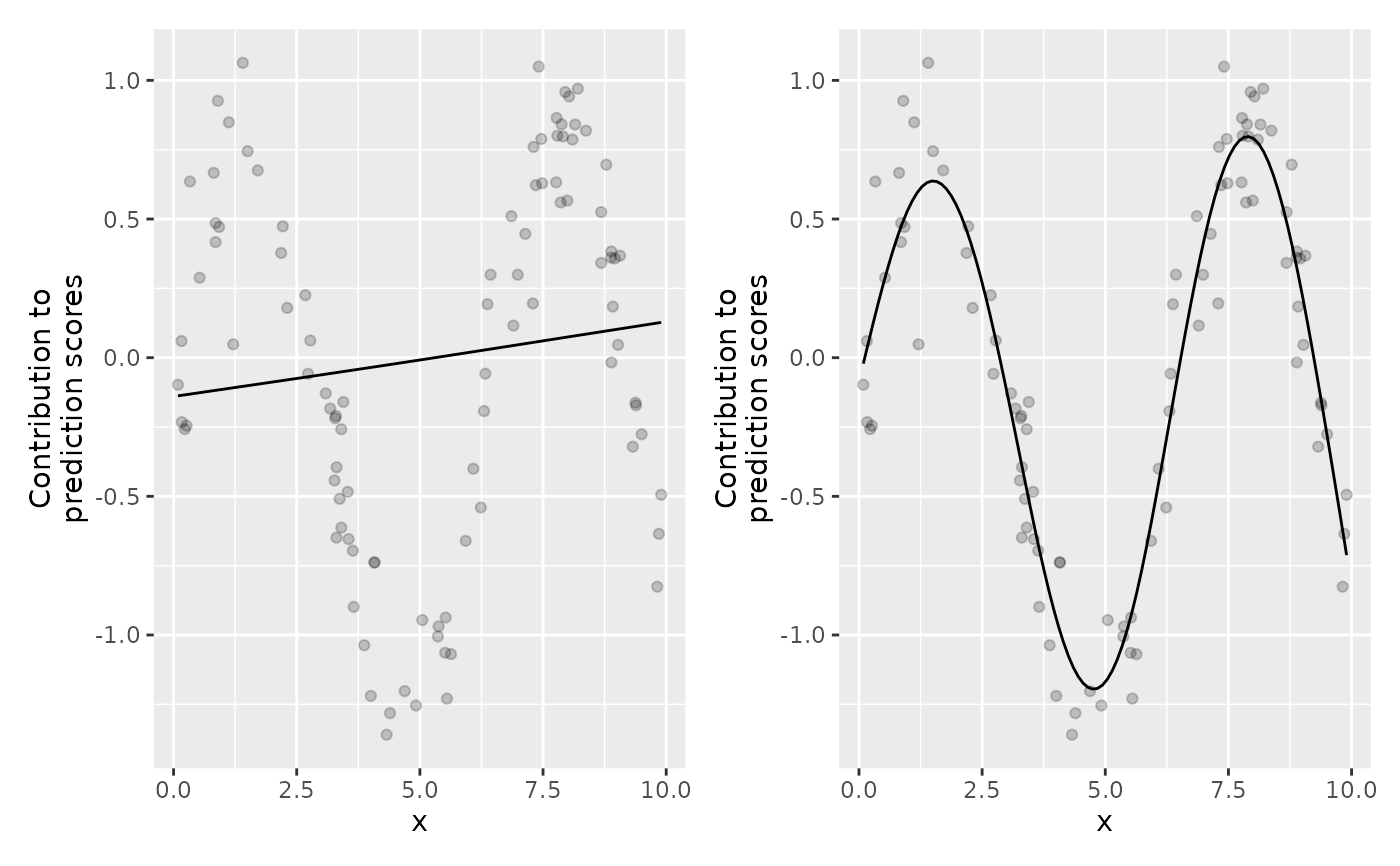
gg_df2 = plotPEUni(cboost_df2, "x")
gg_df5 = plotPEUni(cboost_df5, "x")
library(ggplot2)
library(patchwork)
(gg_df2 | gg_df5) &
geom_point(data = dat, aes(x = x, y = y - c(cboost_df2$offset)), alpha = 0.2)